Explaining a Kaplan-Meier Curve

Edited: June 27, 2019

This is not true

At every point, the curve is equal to “the number of people who we know were alive on day x” divided by “the number of people we know were enrolled on day x”.

I have since spent some quality time with wikipedia and it's a little more complex - and less likely to always go to 0. more soon.

---

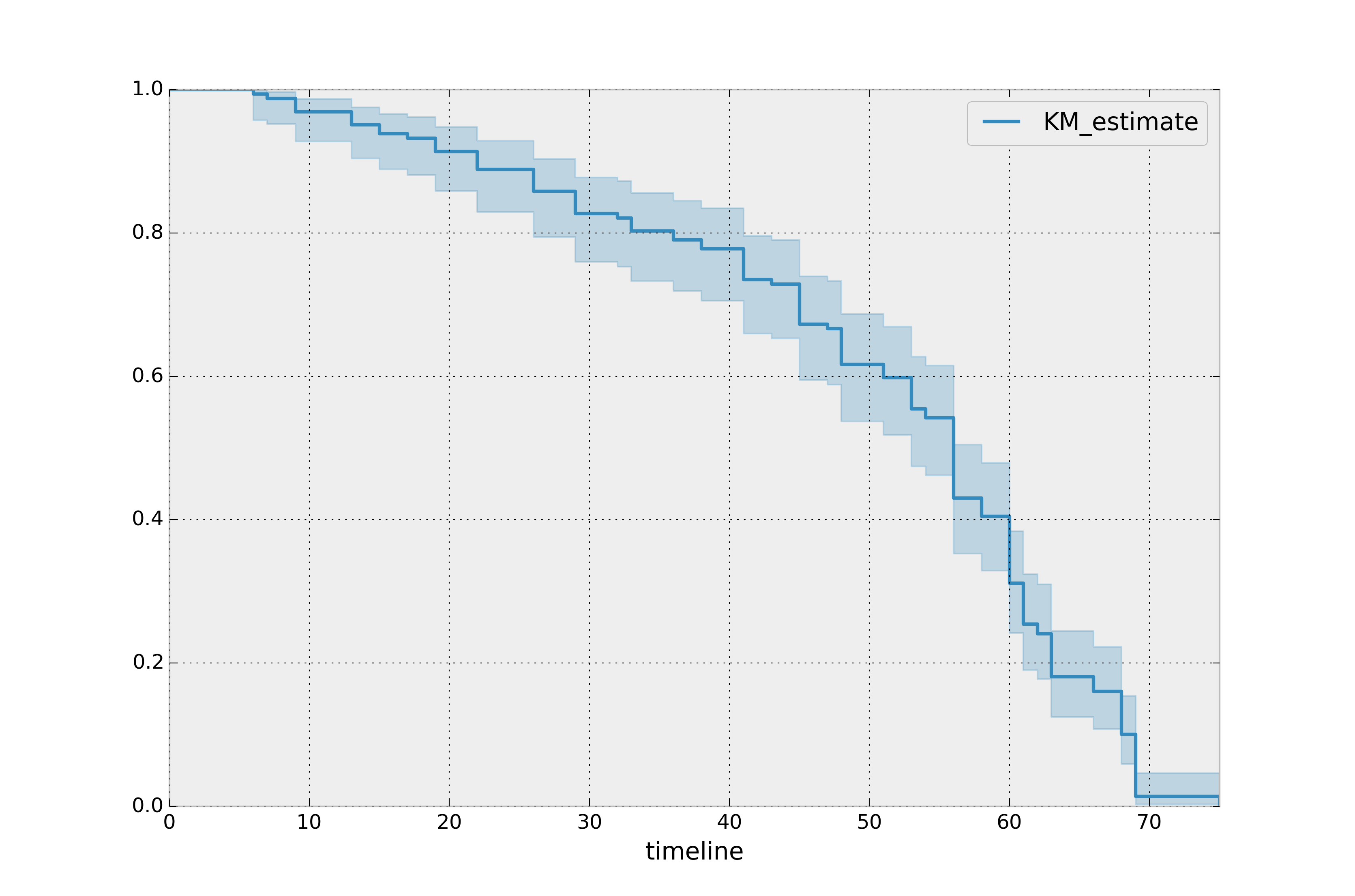Example curve from Lifelines Quickstart Documentation

Let's assume the timeline is in days. At every point, the curve is equal to "the number of people who we know were alive on day x" divided by "the number of people we know were enrolled on day x".

So the first few days, all the people are alive, n/n = 1.

Then on say, day 20, the estimate is about 0.9. 90% of the people enrolled at least 20 days were alive on the 20th day. 9 out of 10.

This works with right-censoring because people can drop out of the denominator when they are censored - if it was exactly 10 people on day 20 and one of those people was only enrolled for 20 days at measurement, when we go to calculate day 21, if there were no deaths, we would lose one person from both the numerator and the denominator: 8/9

Day 20: We have knowledge about 10 people, 1 of whom died, survival rate is 0.9

Day 21: We lose knowledge of 1 person. We have knowledge about 9 people, 1 of whom died, survival rate is 0.88

The curve is strictly decreasing because you lose people from the numerator the same or more than you lose them out of the denominator. If you lose someone due to censoring, you lose one out of both the numerator and the denominator, as in my example. If you lose someone due to death, you only lose them out of the numerator.

(a+1)/(b+1) ? a/b

b(a+1) ? a(b+1)

ab + b ? ab + a

a is always leq b because you can't know about more alive people than all the people you know about. so (a+1)/(b+1) is always geq a/b.